<2019年の鷗友学園>
AさんとBさんとCさんの3人が同時に学校を出発し、公園まで向かいます。
Aさんが公園についた15分後にBさんが公園に着きます。
AさんとBさんはそれぞれ一定の速さで走り、Aさんの速さはBさんの速さの2倍です。
Cさんは初めにAさんの4分の1の速さで歩き、途中からBさんの3倍の速さで走ります。
Cさんが公園に2番目以内に着くようにするには、スタートして何分以内に走り始めればよいですか。

算数の予備問で似たような問題が・・・。是非チャレンジしてください。
ヒント:2800mの道のりをはじめは分速40mで進み、途中で分速80mで進むと30分後に到着します。
分速40mで進む時間は何分間でした
ヒントは隠しているので見たい時は、マウスをドラッグして下さい。。
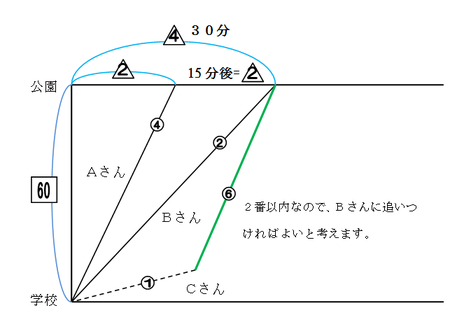
A:B=②:①
A:C=④:①(歩き)
A:B:C=④:②:①
Cの走る速さはBの3倍なので、⑥
AとBの時間の差が15分なので、
(逆比)A:Bの時間の比=2:4
この差が15分間なので、時間が求められます。
Aさん=15分
Bさん=30分
学校から公園までの距離=15分×Aさんの速さ④=60とおきましょう。

「つるかめ算」
かかる時間=30分
学校から公園までの道のり=60
歩きの速さ=①
走る速さ=⑥
<答え>
24分以内
